From playground spats and friendly bets to the 50-yard line at the Superbowl, coin flips are a cultural cornerstone, a time-honored way to reach a fair decision.
But how can you be sure that a coin flip is fair? Maybe your coin-flipping adversary, knowing that you place too much faith in the “tails never fails” strategy, swapped out the worn nickel you agreed to use for an unevenly weighted replica right before the toss. Or maybe you’re planning to perform a completely honest flip that will settle a wager with a friend on the other side of the world, but she is overcome with suspicion. Is there a way to prevent an opponent from cheating, or, alternatively, to convince a friend that you’re being honest?
It turns out that this mutual mistrust can’t be overcome—at least, not with an ordinary coin. But what if you instead used a quantum “coin”—something like an atom or a photon that obeys the rules of quantum physics?
In 2007, a paper appeared on the open-access preprint server arXiv.org that addressed this question. In 80 quirky pages, Carlos Mochon, then a postdoctoral researcher at the Perimeter Institute, supplied the answer: Yes, it’s possible for both parties to be convinced that a quantum coin flip is fair. But unfortunately, Mochon provided only the answer—not a complete method for actually performing a fair flip.
“It's always very interesting to me when we have such a simple question that leads to such complex solutions,” says Carl Miller (in photo), a Fellow of the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland and a mathematician at the National Institute of Standards and Technology (NIST).
Miller learned of Mochon’s result, which was never published in a peer-reviewed journal, from a seminar he attended at UC Berkeley in 2014. By then, Mochon had left academia, and his quantum coin flipping proof had only recently been streamlined and published by a team of five other researchers. Since then, other progress has been made, but an efficient protocol for performing fair flips remained elusive.
“My original goal was to construct a protocol,” says Miller. “I was coming up with these theoretical models in order to do that, and I was running into this obstruction. I couldn’t figure out why I couldn’t get it to be as efficient as I wanted.”
In a new paper, recently presented at the 23rd Annual Conference on Quantum Information Processing and accepted at the 52nd Annual Symposium on the Theory of Computing, Miller found the answer, 12 years after Mochon’s original work. He proved that mutual mistrust can be overcome only by passing the coin back and forth an exorbitant number of times, a result that ensures fair quantum coin flipping protocols will always be too inefficient to use in practice.
In particular, Miller proved that a fair coin toss could only be guaranteed if the coin gets passed back and forth between the two flippers a number of times that grows exponentially with the desired fairness (more fairness means less bias). This was already known to be the worst case, but Miller was the first to show that it’s also the best you can do.
To carry out his proof, Miller relied on a kinship between coin flipping protocols and mathematical tools called point games.
Point games are kind of like a solo game of checkers, and we can even visualize them on a checkerboard. They’re tools for studying probability distributions (the things that represent coins in the abstract) that are subject to certain rules. Researchers previously discovered a connection between point games and coin flipping, and Miller hoped that this connection might provide the right language for constructing efficient protocols.
Point games have just a few parts. They have an initial configuration—a particular arrangement of checkers—and a final configuration, and they progress from one to the other via a series of valid moves. This mimics the procedure of a coin flipping protocol, with each valid move corresponding to a communication between the two parties. Ultimately, the two parties ought to agree that the coin is fair, which corresponds to a particular final configuration in the point game.
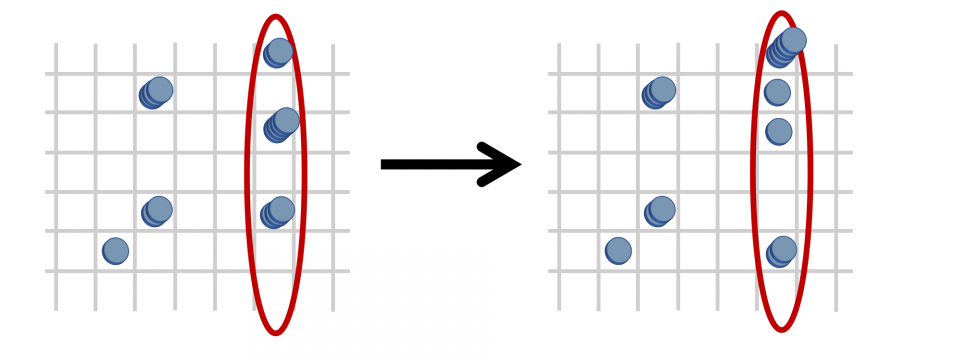
Imagine a bunch of checkers placed on a two-dimensional grid. Roughly speaking, a point game is a sequence of valid moves of these checkers. Each move consists of rearranging checkers that lie in the same row (horizontal move) or the same column (vertical move), such that their average distribution along those lines doesn't get smaller. (There are a few more technical rules, too, and you can read about them in the paper.) (Credit: C. Miller/QuICS)
Miller found that getting close to an unbiased probability distribution requires a point game with many, many moves. And, as a direct consequence, any coin flipping protocol would require many, many rounds of communication to guarantee fairness.
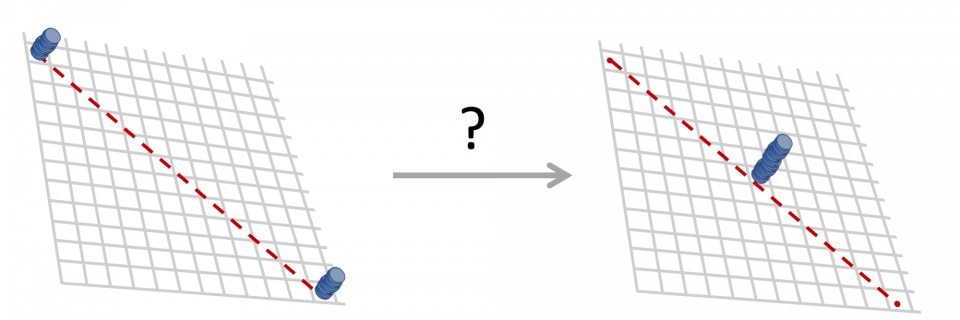
The fair coin flipping problem reduces to this: Can we start with two equal stacks of checkers (as shown in the diagram on the left) and use valid moves to reach the arrangement on the right (which is just above the midpoint of the original stacks)? The answer: Yes, but it will take an exponential number of moves. (Credit: C. Miller/QuICS)
A surprising aspect of Miller’s proof, which is more involved than the overview here, is how little it relies on the fact that the coin or the two parties are quantum. “In order to explain the problem to an adept math student, you wouldn’t need to mention quantum at all,” he says. “You could just pose it as an elegant, neat math puzzle for someone to solve.”
Miller says he hasn’t quite given up on the search for an efficient protocol, which could still be possible if both parties are willing to accept a little bias. “We will never get the bias close to zero,” he says, “but some recent work examines what happens if we allow, say, 10% bias.”
Miller also mentioned the possibility of introducing more constraints on the two coin-flipping parties, limiting their power to cheat and thus decreasing the amount of communication they need to ensure fairness. One idea is to enforce a physical constraint—like the speed of light—and study the effect it has on protocol efficiency. “Maybe we can change the model in a way so that this impossibility result would no longer apply, and we can do efficient coin flipping after all,” Miller says. “The communication model might be more complex, but the crucial thing is that if we assume the speed of light limit holds, we might actually enable security proofs that would not otherwise be possible.”
QuICS is a partnership between the University of Maryland and NIST. It receives technical and administrative support from the University of Maryland Institute for Advanced Computer Studies.
—Story by Chris Cesare